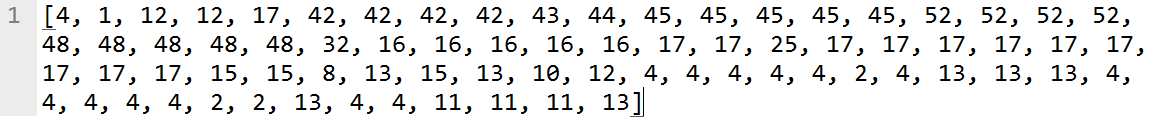Hand Gesture

Hand Gesture Recognition uses Computer Vision, Image Processing and Machine Learning to detect gestures using which specific actions can be performed. The aim of this project was “To create a dynamic hand gesture recognition system that recognizes a set of gestures and performs a corresponding action”.

The following diagram gives a high level overview of the architecture of this project.

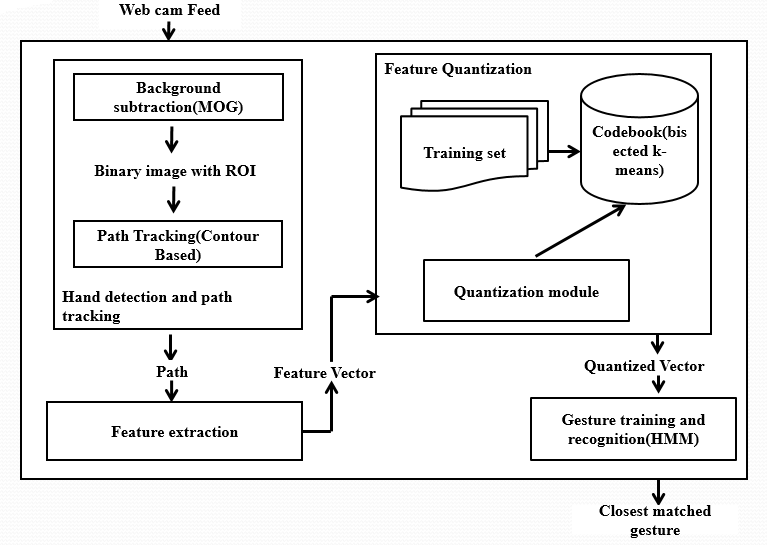
At a high level, the movement of hand is tracked, the path traversed by it is matched against trained gestures and the best gesture is selected, also performing its associated action.

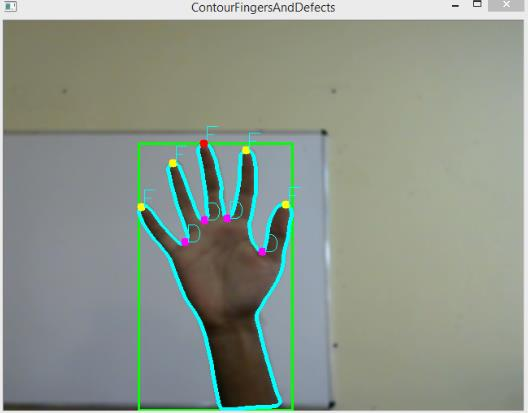
##Detection of Hand Contour In order to detect various gestures performed by hand, the hand as a contour has to be detected first. The hand has to be detected as an outline or a silhouette. The input image frames from web camera is processed using Mixture of Gaussian background subtraction. The obtained mask is then used to detect contours and identify fingers.

Background model

Foreground object

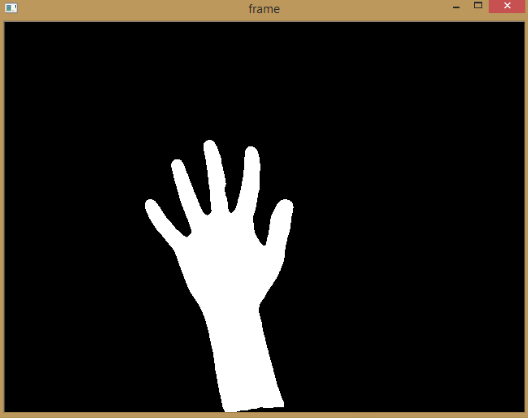Foreground mask

##Finger detection Next, fingers are detected by looking for immediate peaks and defects. The peaks and defects found are then validated to check if they really represent fingers. If found so, they are marked and the movement of highest finger is tracked.

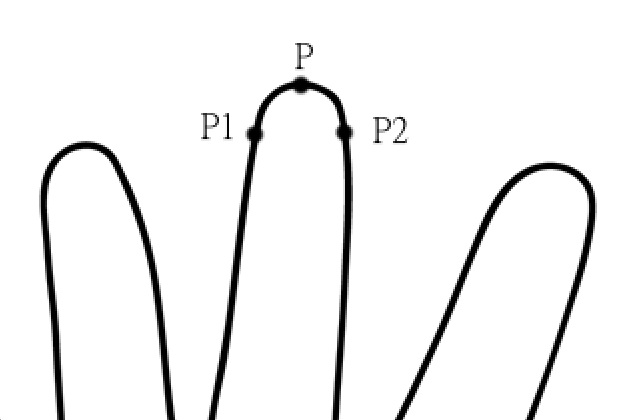Potential Peak

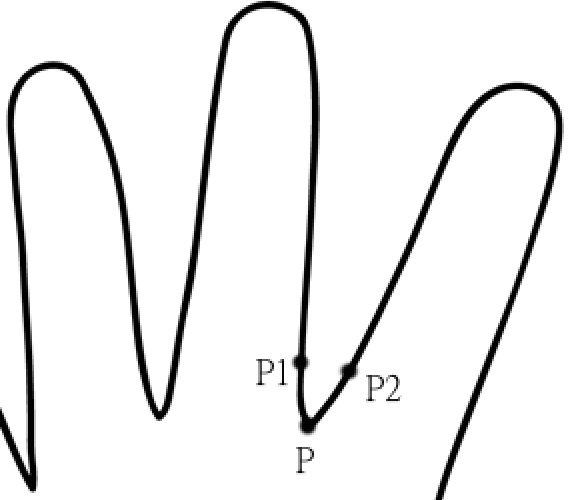Potential Defect

When the movement data is collected incrementally, we get a sequence of coordinates where the tip of the finger has moved.

Tracked path (Points)

##Feature extraction The obtained path, or the set of points, is very specific to the canvas on which a gesture is made. In other words, if we use this representation as it is, we will not be able to differenciate between a “small” and a “large” gesture as they become fundamentally different. So, they are subjected to feature extraction. In this step, a known list of size-independent features are extracted and they are further used in representing this gesture. For each point in the gesture path, the following features are extracted.

1. Location (distance) relative to Centre of gravity of the path of the gesture.
2. Angle with Centre of Gravity of the path of the gesture.
3. Angle with the initial point of the path of the gesture.
4. Angle with the ending point of the path of the gesture.
5. Angle with the bottom left corner of the path of the gesture.
6. Angle with the top left corner of the path of the gesture.
7. Angle with the bottom right corner of the path of the gesture.
8. Angle with the top right corner of the path of the gesture.

Thus, for N points in gesture path, a Nx2 array is now transformed into a Nx8 array. Example:

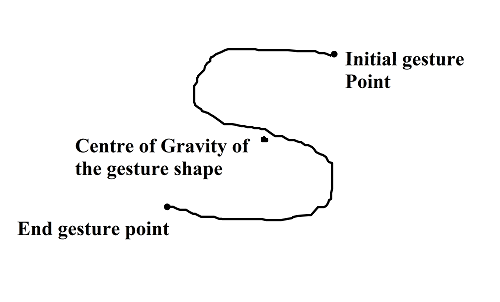Example Gesture Path

Gesture represented as points

Gesture represented as feature vectors

##Training gestures For training gestures, the set of all feature vectors obtained from every training gesture is subjected to k-means clustering to obtain a set of cluster centroids and they are saved as “Codebook”. This codebook acts as a ready reckoner later for identifying gestures. Here, we select k=64, so that, 64 centroid locations are obtained. Each centroid is given an index, starting from 0 to 63.

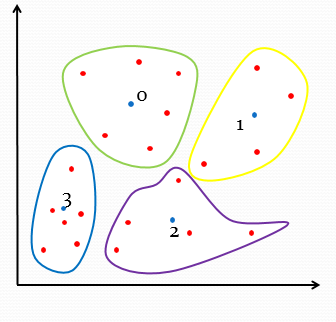Quantization

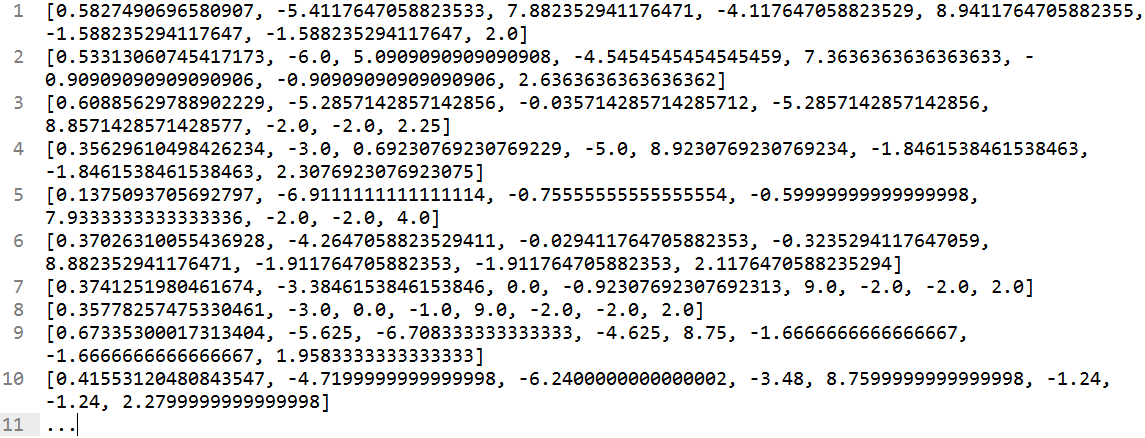k-means clustering (location of centroids)

After this, for each training gesture, its feature vector representation is quantized, or each point in the multidimensional feature plane is replaced with the index of nearest cluster, essentially transforming a gesture into a sequence of indices (integers).

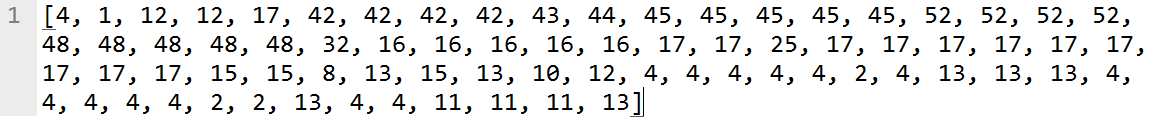A gesture represented as a sequence of cluster indices

This sequence, or “states”, is fed to train a Hidden Markov Model using Baum-Welch algorithm. This populates the parameters of an empty Hidden Markov Model by computing the probability distribution from each state to the other. Baum-Welch algorithm works by “expecting” and then “maximizing” the model parameters for a given sequence of states. The obtained Hidden Markov Model parameters are then saved. The following are the parameters of a Hidden Markov Model which are saved:

1. N - The number of states in the model.
2. M - The number of distinct observation symbols per state. It is also called as the discrete alphabet size.
3. A - The state transition probability distribution. i.e. the probability of transition from one state to another.
4. B - The observation symbol probability distribution. i.e. the probability of emitting a particular observation symbol in a given state.
5. Pi - The initial state distribution

More details about Hidden Markov models can be found here. In a nutshell, given a sequence of states, Baum-Welch algorithm computes the above parameters.

##Recognizing a gesture To recognize a gesture, its quantized representation is fed to Viterbi algorithm that computes the probability of a sequence with respect to every saved Hidden Markov Model. Given a Hidden Markov Model and an Observation Sequence, it calculates the probability that the Observation Sequence was generated by the given Hidden Markov Model. The model that has the highest probability is the recognized gesture.

##Screenshots This was originally intended to be used by specially abled people for communication, but it can be used on any x86 or amd64 machine with a camera device by anyone.

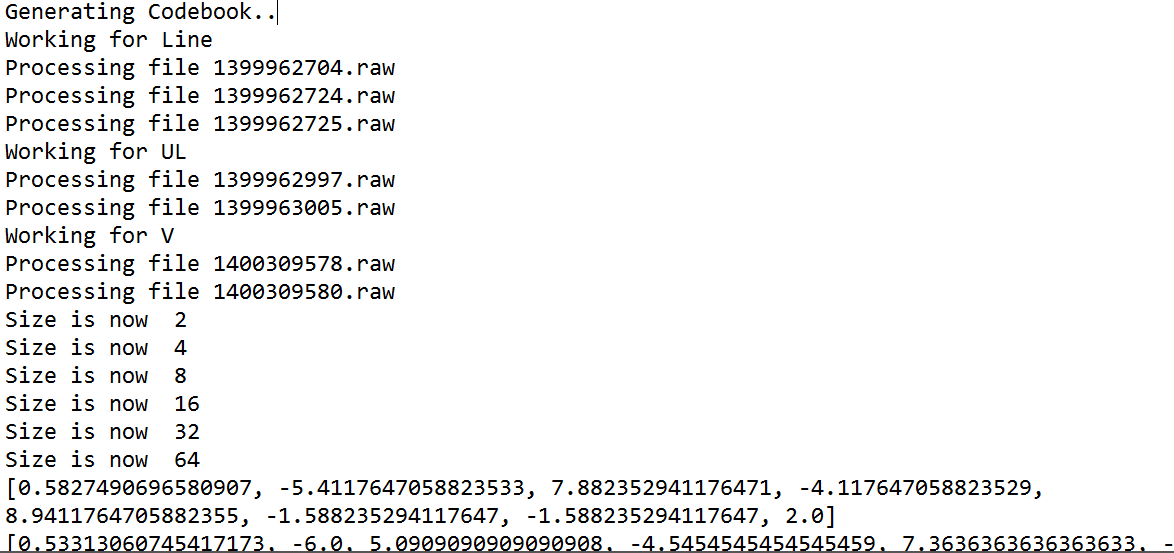Codebook generation

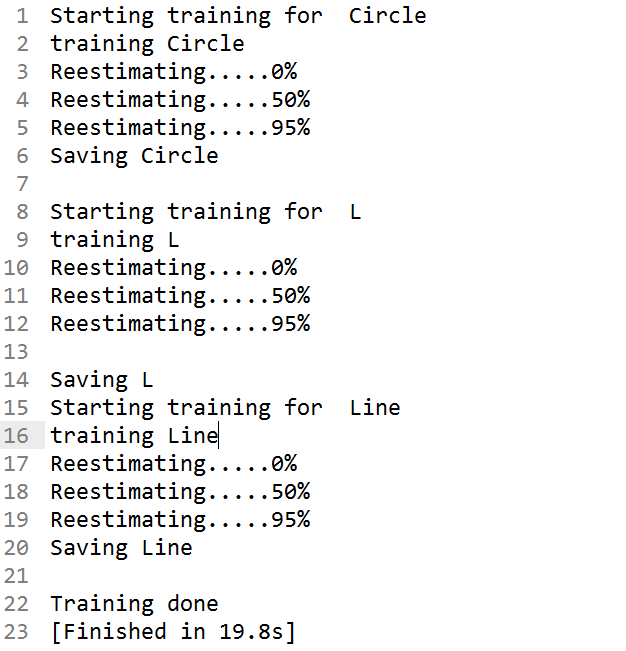Hidden Markov Model training using Baum-Welch algorithm

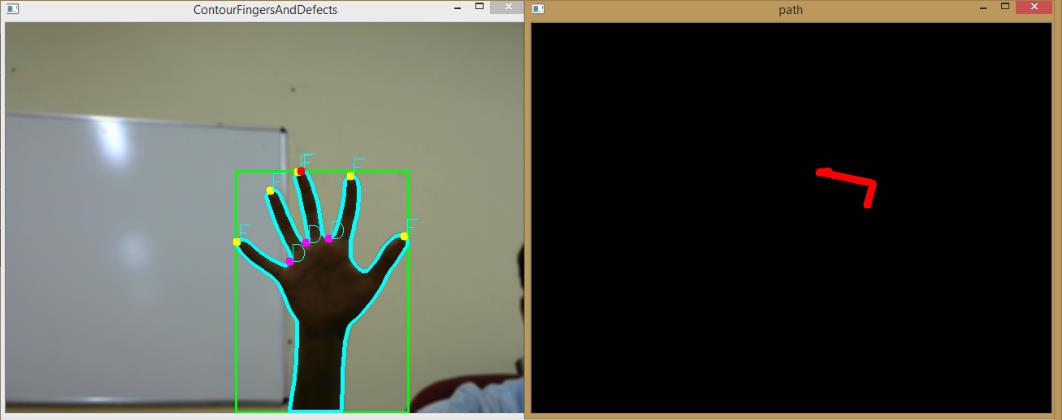Gesture started

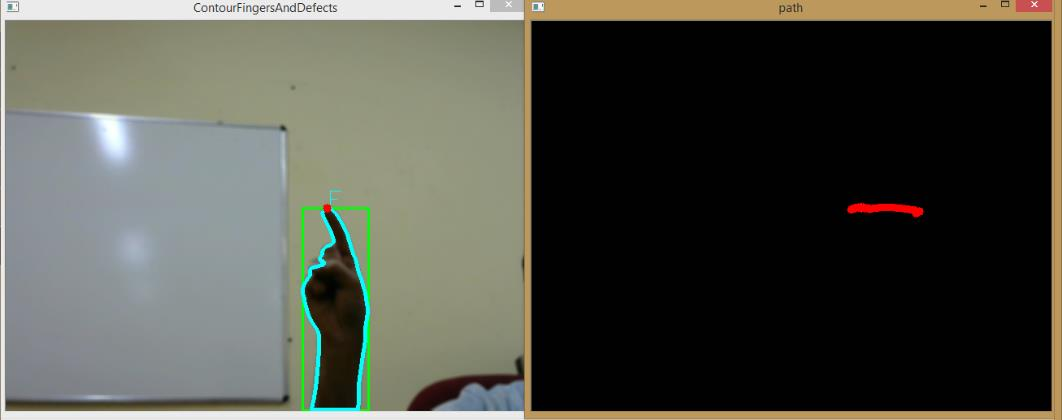Gesture in progress

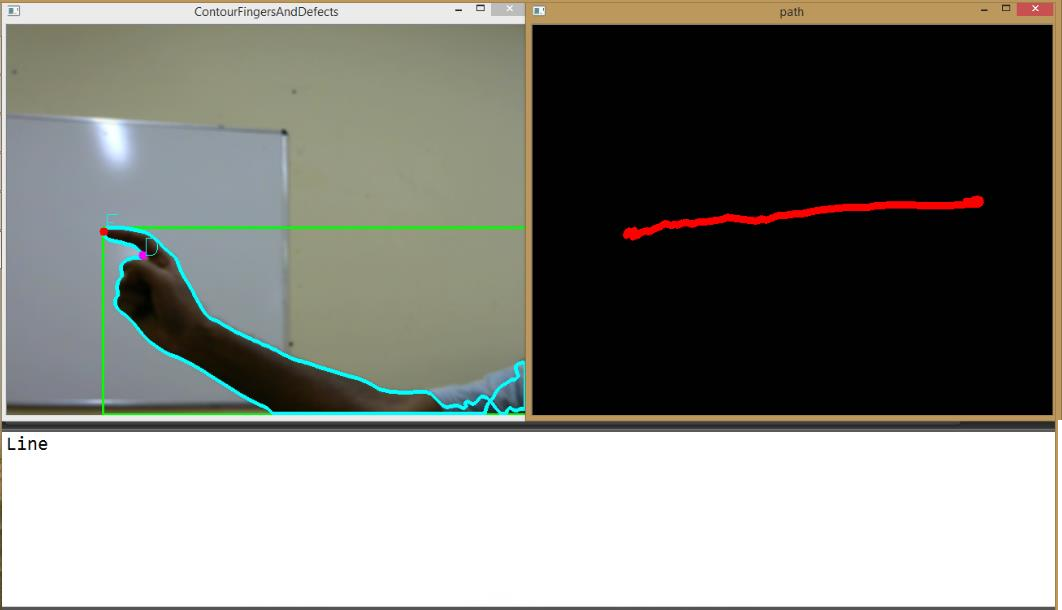Gesture completed - recognized gesture is Line

The following document provides more details if required: